2 Answers

Anuith · Answer 1 · 2018-08-27T21:34:24+0000

Answer:

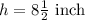
$h=8(1)/(2)\text{ inch}$

Explanation:

Let h represent height of prism.

We have been given that Tana fills the prism with base lengths
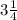3(1)/(4) inch and
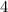inch with a
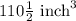$110(1)/(2)\text{ inch}^3$ .

We know that volume of prism is area of base times height, so we can set an equation as:

$\text{Volume of prism}=\text{Base length}*\text{Base width}* \text{Height of prism}$

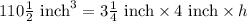
$110(1)/(2)\text{ inch}^3=3(1)/(4)\text{ inch}* 4\text{ inch}* h$

$(221)/(2)\text{ inch}^3=(13)/(4)\text{ inch}* 4\text{ inch}* h$

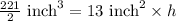
$(221)/(2)\text{ inch}^3=13\text{ inch}^2* h$

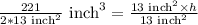
$\frac{221}{2*13\text{ inch}^2}\text{ inch}^3=\frac{13\text{ inch}^2* h}{13\text{ inch}^2}$

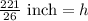
$(221)/(26)\text{ inch}=h$

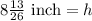
$8(13)/(26)\text{ inch}=h$

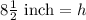
$8(1)/(2)\text{ inch}=h$

Therefore, the height of the prism is
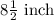$8(1)/(2)\text{ inch}$ .

Please log in or register to add a comment.