The compound inequality will be:
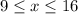 , where
, where
 is the mass of a single pencil and each pencil can have a mass of 10.5 grams.
is the mass of a single pencil and each pencil can have a mass of 10.5 grams.
Step-by-step explanation
Suppose, the mass of a single pencil in the pack is
 gram.
gram.
So, the total mass of 5 pencils will be:
 grams.
grams.
Each package has a mass of 15 grams. So, the total weight of the pack of 5 pencils
 grams.
grams.
To be within the weight specifications, a pack of 5 pencils should weigh between 60 grams and 95 grams. So, the compound inequality will be..........
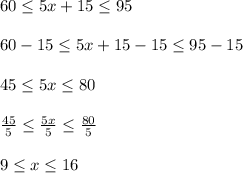
So, the compound inequality to represent the mass of a single pencil in a pack will be:
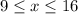 , where
, where
 is the mass of a single pencil.
is the mass of a single pencil.
- As 10.5 grams lies inside the interval
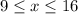 , so each pencil can have a mass of 10.5 grams.
, so each pencil can have a mass of 10.5 grams.