Question

How many positive 4-digit integers have only odd digits?

Answer 1

`5^4 = 625`

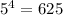
Explanation:

There are 5 possible odd digits to choose from: 1,3,5,7,9.

When we chose our first digit, we have 5 choices (the possible odd digits). For every one of those 5 choices, we can chose our second digit in 5 different ways again, then we have 5*5 = 25 ways for choosing our first two digits. We can do the same again, as for every one of the 25 first two digits, we can chose our third digit in 5 different ways (again, the odd numbers). So we multiply it by 5 again. Repeating this one more time, because we have 5 different ways to chose our fourth digit. At the end we will have

`5*5*5*5 = 5^4 = 625`

This is a commun counting technique.