Question

Which expression results when the change of base formula is applied to log4(x+2) ?

Answer 1

`(\log (x+2))/(\log 4)` is the correct answer.

Solution-

The formula for change of base in logarithm is given by,

`\log_(b)a=(\log_(c)a)/(\log_(c)b)`

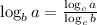
If we take the common base as 'e' , the formula becomes,

`\log_(b)a=(\log a)/(\log b)`

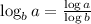
Applying this formula,

`\log_(4)(x+2)=(\log (x+2))/(\log 4)`

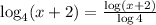
∴ As the first option matches with our answer, hence it is the correct answer.

( In the fourth option a bracket is missing, so it is not the correct option)