Question

Any proposed solution of a rational equation that causes a denominator to equal​ _______ is rejected.

Answer 1

A proposed solution of a rational equation that causes a denominator to equal zero is rejected because division by zero is not possible.

Step-by-step explanation:

Any proposed solution of a rational equation that causes a denominator to equal zero is rejected. When the denominator of a rational equation is zero, the fraction becomes undefined because division by zero is not possible. In mathematics, division by zero is an undefined operation.

Answer 2

Any proposed solution of a rational equation that causes a denominator to equal​ __ZERO__ is rejected.

Step-by-step explanation:

We will show this statement is true by an example:

Consider the expression :
`(x)/(x-4)=(x)/(x-4)+4`

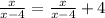
Now, solved the rational expression and check its proposed solution

`(x)/(x-4)=(x)/(x-4)+4`

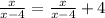
x cannot equal to 4, as it makes both denominators equal to zero.

Multiply both the sides by (x-4),

`\left ( x-4 \right )\cdot (x)/(x-4)=\left (x-4 \right )\cdot\left ( (x)/(x-4)+4  \right )\\`

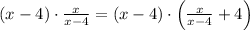
Now, use the distributive property on Right hand side,

`\left ( x-4 \right )\cdot (x)/(x-4)=\left (x-4 \right )\cdot \left ( (x)/(x-4) \right )+\left (x-4 \right )\cdot 4\\`

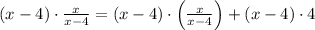
Simplify the above expression,

`x=x+4x-16`

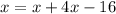
Combine like terms,

`x-x-4x=-16`

`-4x=-16`

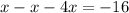
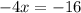
Divide both sides by -4, we get

`(-4x)/(-4)=(-16)/(-4)`

`x=4`.

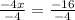
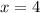As we know that x cannot equal to 4, replacing x=4 in the original expression causes the denominator equal to 0.

Check the solution:
`(x)/(x-4)=(x)/(x-4)+4`

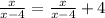
Substitute the value of x=4 in the original expression,

`(4)/(4-4)=(4)/(4-4)+4`

`(4)/(0)=(4)/(0)+4`

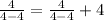
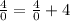
Thus, 4 must be rejected as the solution, and the solution set is only 0.