Question

Identify the coordinates of the vertex and focus, the equations of the axis of symmetry and directrix, and the direction of opening of the parabola with the given equation. Then find the length of the latus rectum and graph the parabola.

Answer 1

Equation of the Parabola

The equation of a parabola with vertex at (h, k) with its axis of symmetry in the vertical direction is:

`4p(y-k)=(x-h)^2`

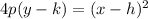
Where p is the distance from the vertex to the focus and also the distance from the vertex to the directrix.

We are given the equation:

`y=(x-4)^2+3`

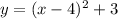
Rewriting:

`y-3=(x-4)^2`

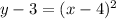
This corresponds to a parabola that opens up with its vertex located at V(4,3).

The value of 4p = 1 gives :

`p=(1)/(4)`

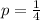
The axis of symmetry is a vertical line that passes through the vertex, that is, the line x = 4.

Since the parabola opens up, the focus is 1/4 units above the vertex, i.e., it's located at:

`F\mleft(4,3+(1)/(4)\mright)=F\mleft(4,(13)/(4)\mright)`

The directrix is a horizontal line located 1/4 units below the vertex, thus its equation is:

`\begin{gathered} y=3-(1)/(4) \\ y=(11)/(4) \end{gathered}`

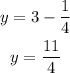
The length of the latus rectum is defined as 4p. Since p=1/4, then 4p = 1

The graph of the parabola is: