Question

Team Arrow shoots an arrow from the top of a 1500-foot building on Earth-68. The arrow reaches amaximum height of 2000 feet after 5 seconds.Write an equation for the height of the arrow, h, in feet as a function of the number of seconds, t, since the arrow was shot.Round to 3 decimal places as needed.After how many seconds will the arrow reach the ground?Round to 3 decimal places as needed.

Answer 1

The trajectory of the arrow is a parabola, therefore, the height "y" as a function of time "t" is of the following form:

`y=y_0+bt-(1)/(2)gt^2`

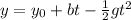
Where y0 is the initial height and "g" is the acceleration of gravity and is equal to:

`g=32(ft)/(s^2)`

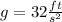
Replacing we get:

`y=1500+bt-16t^2`

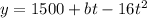
Now, to determine the value of "b" we need to have into account that the arrow will reach its maximum height when it passes through the vertex of the parabola. As shown in the following diagram:

The vertex is given by:

`t_v=-(b)/(2a)_{}`

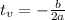
Where "a" and "b" are determined from the equation using the following general form:

`y=c+bt+at^2`

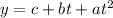
Replacing the value in the formula for the height:

`2000=1500+b(-(b)/(2a))-16(-(b)/(2a))^2^{}`

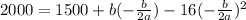
Simplifying:

`2000=1500-(b^2)/(2a)-(4b^2)/(a^2)`

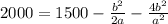
subtracting 1500 to both sides:

`1500=-(b^2)/(2a)-(4b^2)/(a^2)`

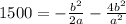
Now we take b squared as a common factor:

`1500=b^2(-(1)/(2a)-(4)/(a^2))`

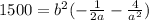
Now we divide by the factor at the right of b square:

`(1500)/(-(1)/(2a)-(4)/(a^2))=b^2`

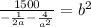
Taking square root to both sides:

`\sqrt[]{(1500)/(-(1)/(2a)-(4)/(a^2))}=b^{}`

Replacing the value of a:

`\sqrt[]{(1500)/(-(1)/(2(-16))-(4)/((-16)^2))}=b`

Solving the operation:

`b=309.8`

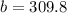
Replacing in the initial function of "y" vs "t":

`y=1500+309.8t-16t^2`

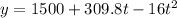
This is the equation of the height as a function of time.

To determine the time for the arrow to reach the ground we need to set the equation to zero:

`0=1500+309.8t-16t^2`

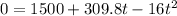
Using the quadratic formula:

`t=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}`

Replacing the values: