Question

If r = x, y, z and r0 = x0, y0, z0 , describe the set of all points (x, y, z) such that |r − r0| = 5.

Answer 1

Point
`\left ( x,y,z\right )` represents a sphere

Explanation:

Take
`r=\left ( x,y,z \right )\,,\,r_0=\left ( x_0,y_0,z_0 \right )`

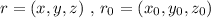
We need to describe the set of all points (x, y, z) such that
`\left | r-r_0 \right |=5`

Solution :

For
`r-r_0=\left ( x,y,z \right )-\left ( x_0,y_0,z_0 \right )`, we will subtract the respective elements .

`r-r_0=\left ( x,y,z \right )-\left ( x_0,y_0,z_0 \right )=\left ( x-x_0,y-y_0,z-z_0 \right )`

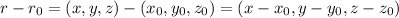
Therefore,
`\left | r-r_0 \right |=√((x-x_0)^2+(y-y_0)^2+(z-z_0)^2)`

As
`\left | r-r_0 \right |=5`, we get

`√((x-x_0)^2+(y-y_0)^2+(z-z_0)^2)=5`

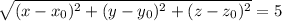
On squaring both sides, we get

`\left ( √((x-x_0)^2+(y-y_0)^2+(z-z_0)^2) \right )^2=5^2\\(x-x_0)^2+(y-y_0)^2+(z-z_0)^2=25`

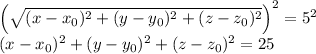
The general equation of a sphere is (x - a)² + (y - b)² + (z - c)² = r², where (a, b, c) denotes the center of the sphere and r represents the radius .

So,
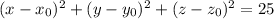`(x-x_0)^2+(y-y_0)^2+(z-z_0)^2=25` represents a sphere with center as
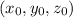`\left ( x_0,y_0,z_0 \right )` and radius equal to 5 units

Answer 2

We are concern about the vector (x-x0, y-y0, z-z0) equaling to 5.

This happens when √(x-x0)^2 + (y-y0)^2 + (z-z0)^2 = 5

Square both side:

(x-x0)^2 + (y-y0)^2 + (z-z0)^2 = 25 , a sphere

Which you will recognize as a circle of radius one centered at (x0, y0, z0)