Question

Please help solve this:
`3^(x + 1) = 100`

Answer 1

remember, you can do anything to an equaiton as long as you do it to both sides

also

`log(a^x)=xlog(a)`
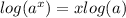
and
`ln(x)=log_e(x)`
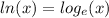
ok
if no base is stated, assume log=
`log_(10)`
I'm going to use ln instead of log because ln is easier to find on a calculator


`3^(x+1)=100`
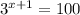
take ln of both sides

`ln(3^(x+1))=ln(100)`

`(x+1)ln(3)=ln(100)`

`xln(3)+1ln(3)=ln(100)`
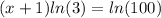
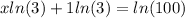
minus ln(3) both sides

`xln(3)=ln(100)-ln(3)`
divide both sides by ln(3)

`x=(ln(100))/(ln(3))-1`

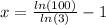
or if you wanted to use log base 10

`3^(x+1)=100`
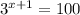
take log both sides

`log(3^(x+1))=log(100)`

`log(3^(x+1))=2`

`(x+1)log(3)=2`

`xlog(3)+log(3)=2`
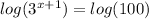
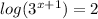
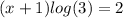
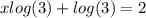
minus log(3) both sides

`xlog(3)=2-log(3)`
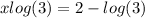
divide both sides by log(3)

`x=(2)/(log(3))-1`



so

`x=(ln(100))/(ln(3))-1`
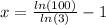
or if you wanted log

`x=(2)/(log(3))-1`