Question

If m<1 = 7x + 6 and m<2 = 8x - 6, find the value of x so that p is perpendicular to q

Answer 1

x = 12

Explanation:

Given:
`\angle 1=7x+6`

`\angle 2=8x-6`

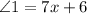
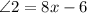
∠1 and ∠2 form by two intersection line p and q.

p is perpendicular to q.

Therefore, ∠1 = ∠2 = 90°

So, 7x + 6 = 90°

7x = 84

x = 12

8x - 6 = 90°

8x = 96

x = 12

7x + 6 = 8x - 6

x = 6 + 6

x = 12

So, we get x=12 from all three equations.

hence, The value of x is 12