Question

Find an equation for the nth term of the arithmetic sequence.

a16 = 21, a17 = -1

an = 351 + 22(n + 1)
an = 351 - 22(n + 1)
an = 351 + 22(n - 1)
an = 351 - 22(n - 1)

Answer 1

so it went from the 16th term to the 17th term, and went from 21 to -1... what would the "common difference" d be then?

le'ts see


`\bf a_(16)=21\quad and\quad a_(17)=-1 \\\\\\ a_(16)+d=-1\implies 21+d=-1\implies d=-1-21\implies \boxed{d=-22}`

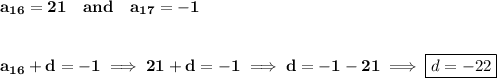
alrite.. so d = -22.. hmm what would the first term be then?


`\bf n^(th)\textit{ term of an arithmetic sequence}\\\\ a_n=a_1+(n-1)d\qquad \begin{cases} n=n^(th)\ term\\ a_1=\textit{first term's value}\\ d=\textit{common difference}\\ ----------\\ n=16\\ d=-22\\ a_(16)=21 \end{cases} \\\\\\ a_(16)=a_1+(16-1)\boxed{-22}\implies 21=a_1+(16-1)(-22) \\\\\\ 21=a_1+(15)(-22)\implies 21=a_1-330\implies \boxed{351=a_1}\\\\ -------------------------------\\\\ a_n=a_1+(n-1)d\implies \boxed{a_n=351+(n-1)(-22)}`

which of course, you can rewrite as


`\bf {a_n=351+(n-1)(-22)}\implies a_n=351-22(n-1) \\\\\\ or\qquad a_n=351+22(1-n)\implies a_n=351+22-22n`

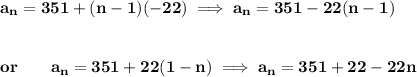
which are all the same.