Question

Suppose that the future price pt) of a certain item is given by the following exponential function. In this function, p(t) is measured in dollars and t is thenumber of years from today.p (t) = 800(1.041)^tFind the initial price of the item.Does the function represent growth or decay?By what percent does the price change each year?

Answer 1

The population function is given below as

`P(t)=800(1.041)^t`

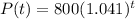
Step 1:

To figure out the initial price of the item, we will substitute the value of t=0

`\begin{gathered} P(t)=800(1.041)^t \\ P(0)=800(1.041)^0 \\ p(0)=800*1 \\ P(0)=800 \end{gathered}`

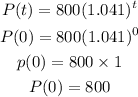
Hence,

The initial pice of the item is = $800

Step 2:

To determine if the function represents a growth or decay, we will use the relation below

The function for exponential growth is given below as

`\begin{gathered} y=ab^t \\ b=1+r(\text{growth)} \\ b=1-r(\text{decay)} \end{gathered}`

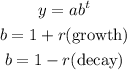
By comparing coefficients, we can see that

`b=1.041>1`

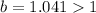
Hence,

The function represents GROWTH

STEP 3:

To figure out the percentage of price change each year, we will use the formula below

`\text{percentage change=}\frac{new\text{ price-initial price}}{in\text{itial price}}*100\%`

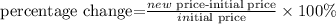
To figure out the thenew price, we will substitute the value of t=1

`\begin{gathered} P(t)=800(1.041)^t \\ P(1)=800(1.041)^1 \\ P(1)=800*1.041 \\ P(1)=832.8 \end{gathered}`

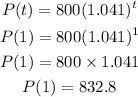
By substituting the values, we will have the percentage to be

`\begin{gathered} \text{percentage change=}\frac{new\text{ price-initial price}}{in\text{itial price}}*100\% \\ \text{percentage change}=(P(1)-P(0))/(P(0))*100\% \\ \text{percentage change}=(832.8-800)/(800)*100\% \\ \text{percentage change}=(32.8)/(800)*100\% \\ \text{percentage change}=(3280)/(800)\% \\ \text{percentage change}=4.1\% \end{gathered}`

Hence,

The percentage = 4.1%