Question

What value of c makes the statement true? -2x3(cx3 + x2) = -10x6 - 2x5

Answer 1

-2x^3(cx^3 + x^2) = -10x^6 - 2x^5

c would have to be 5....because -2x^3(5x^3) = -10x^6

Answer 2

Answer: The required value of c that makes the given statement true is 5.

Step-by-step explanation: We are given to find the value of c that makes the following statement TRUE :

`-2x^3(cx^3+x^2)=-10x^6-2x^5~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~(i)`

To find the value of c, we need to equate the coefficients of the same powers of the unknown variable x.

From equation (i), we have

`-2x^3(cx^3+x^2)=-10x^6-2x^5\\\\\Rightarrow -2cx^(3+3)-2x^(3+2)=-10x^6-2x^5\\\\\Rightarrow -2cx^6-2x^5=-10x^6-2x^5.`

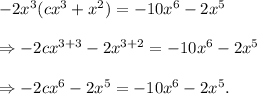
Equating the coefficients of
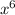`x^6` on both sides of the above equation, we get

`-2c=-10\\\\\Rightarrow c=(-10)/(-2)\\\\\Rightarrow c=5.`

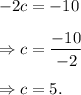
Thus, the required value of c that makes the given statement true is 5.