Answer:
Correct choice is D
Explanation:
Option A. The sum of two fractions is a fraction, a fraction is always rational number.
Option B. The product of a fraction and a repeating decimal can be rational number. For example,
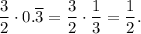
Option C. The sum of a terminating decimal and the square root of a perfect square is always rational number, because the terminating decimal is a decimal that ends and the square root of a perfect square is a natural number. The product of decimal that ends and natural number is rational number.
Option D. The product of a repeating decimal and the square root of a non-perfect square is always irrational, because the square root of a non-perfect square is irrational number and when multiplying irrational number by fraction (any repeating decimal can be written as fraction) you get irrational number.