Question

Determine the equation of the graph and select the correct answer below. parabolic function going down from the left through the point negative five comma zero and turning at the point negative four comma negative one and going up through the point negative three comma zero and through the point zero comma fifteen and continuing towards infinity Courtesy of Texas Instruments y = (x + 4)2 + 1 y = (x + 4)2 − 1 y = (x − 4)2 + 1 y = (x − 4)2 − 1

Answer 1

Solution: The correct option is second option, i.e.,
`y=(x+4)^2-1`.

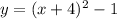Step-by-step explanation:

The standard form of the parabola along the y-axis with vertex (h,k) is
`y=a(x-h)^2+k`.

Since the turning point is given as
`(-4,-1)`.

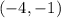Put these values in the standard form of the parabola.

`y=a(x+(-4))^2+(-1)`

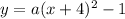`y=a(x+4)^2-1` .....(1)

The parabola passes through the points (-5,0), (-3,0) and (0,15). It means each point will satisfy the above condition.

Put x = 0 and y = 15 in the equation (1).

`15=a(0+4)^2-1\\16=4^2a\\16=16a\\a=1`

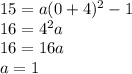
Put a = 1 in equation (1).

`y=1(x+4)^2-1`

Therefore, the The correct option is second option, i.e.,
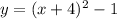`y=(x+4)^2-1`.