Question

Which statements are true about the fully simplified product of (b – 2c)(–3b + c)? Check all that apply. The simplified product has 2 terms. The simplified product has 4 terms. The simplified product has a degree of 2. The simplified product has a degree of 3. The simplified product has a degree of 4. The simplified product, in standard form, has exactly 2 negative terms.

Answer 1

The simplified product has a degree of 2.

The simplified product, in standard form has exactly 2 negative terms.

Explanation:

`(b - 2c)(-3b + c)`

LEts multiply it using FOIL method

`b* -3b= -3b^2`

`b*c= bc`

`(-2c) * (-3b)= 6bc`

`(-2c) * c= -2c^2`

The product is
`-3b^2 +bc+6bc-2c^2`

`-3b^2+7bc-2c^2`

The simplified product has a degree of 2.

It has two negative terms

Answer 2

Answer: The correct options are,

The simplified product has a degree of 2,

The simplified product, in standard form, has exactly 2 negative terms.

Explanation:

Here, the given expression,

`(b-2c)(-3b+c)`

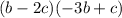
By distributive property,

`=(b-2c)(-3b)+(b-2c)(c)`

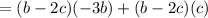
Again by distributive property,

`=b(-3b)-2c(-3b)+bc-2c(c)`

`=-3b^2+6bc+bc-2c^2`

`=-3b^2+7bc-2c^2`

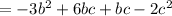
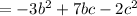
Which is the simplified form of the given expression,

That having three terms in which two terms are negative and the degree ( The highest sum of the exponents of the variables) is 2,

Hence, the correct options are,

The simplified product has a degree of 2,

The simplified product, in standard form, has exactly 2 negative terms.