Question

Prove that if an converges to a nonzero constant then 1/an is bounded

Answer 1

Assume
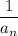
`\frac1{a_n}` is not bounded, i.e. there are no
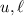
`u,\ell` for which
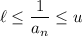
`\ell\le\frac1{a_n}\le u` for all
`n`.

Now,
`a_n\to k\\eq0` is to say that for any
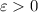
`\varepsilon>0`, we can find a large enough
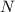
`N` such that
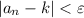
`|a_n-k|<\varepsilon` whenever
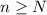
`n\ge N`. Simultaneously, this means that
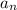
`a_n` is bounded.

Let's suppose without loss of generality that
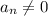
`a_n\\eq0` for any
`n`. (Note that if
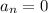
`a_n=0` for some finite number of values of
`n`, we can simply remove them from consideration.)

So we have


`|a_n-k|=\left|a_n\left(1-\frac k{a_n}\right)\right|=|a_n|\left|1-\frac k{a_n}\right|<\varepsilon`

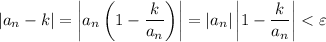
Because
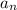
`a_n` is bounded, we know there is some
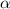
`\alpha` such that
`|a_n|\le\alpha` for all
`n`. Now,


`|a_n|\left|1-\frac k{a_n}\right|\le\alpha\left|1-\frac k{a_n}\right|<\varepsilon`

`\left|1-\frac k{a_n}\right|<\frac\varepsilon\alpha`

`-\frac\varepsilon\alpha<1-\frac k{a_n}<\frac\varepsilon\alpha`

`-1-\frac\varepsilon\alpha<-\frac k{a_n}<-1+\frac\varepsilon\alpha`

`1-\frac\varepsilon\alpha<\frac k{a_n}<1+\frac\varepsilon\alpha`

`\frac1k-\frac\varepsilon{\alpha k}<\frac 1{a_n}<\frac1k+\frac\varepsilon{\alpha k}`

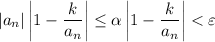
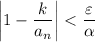
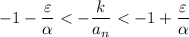
But we initially assumed that
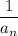
`\frac1{a_n}` is unbounded, so the above is impossible. Thus
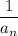
`\frac1{a_n}` must be bounded.