Answer:
The 37th term of arithmetic sequence is 182.
Step-by-step Step-by-step explanation:
Here's the required formula to find the arithmetic sequence :
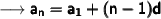
 aₙ = nᵗʰ term in the sequence
aₙ = nᵗʰ term in the sequence
 a₁ = first term in sequence
a₁ = first term in sequence
 n = number of terms
n = number of terms
 d = common difference
d = common difference
Substituting all the given values in the formula to find the 37th term of arithmetic sequence :
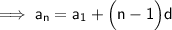
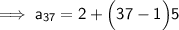
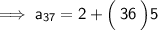
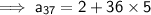
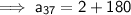
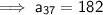
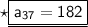
Hence, the 37th term of arithmetic sequence is 182.
