Question

Determine if the graph is symmetric about the x-axis, the y-axis, or the origin. r = 2 cos 5θ

Answer 1

Looking at the graph, we'll notice that there is a local maximum at x=0 and it looks similar on both sides of the y axis, therefore making it symmetric around the y axis given the options

Answer 2

The graph is symmetric about the x-axis.

Explanation:

1. Symmetry about the x-axis: If the point (r, θ ) lies on the graph, then the point (r, -θ ) or (-r, π - θ ) also lies on the graph.

2. Symmetry about the y-axis: If the point (r, θ ) lies on the graph, then the point (r, π - θ ) or (-r, -θ ) also lies on the graph.

3. Symmetry about the origin: If the point (r, θ ) lies on the graph, then the point (-r, θ ) or (r, π + θ ) also lies on the graph.

The given polar equation is

`r=2\cos (5\theta)`

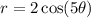
Check the equation by (r, -θ).

`r=2\cos (-5\theta)=2\cos (5\theta)=r`

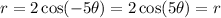
Therefore, the graph is symmetric about the x-axis.

Check the equation by (-r, -θ).

`-r=2\cos (-5\theta)=2\cos (5\theta)=r\\eq -r`

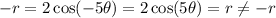
Therefore, the graph is not symmetric about the y-axis.

Check the equation by (-r, θ).

`-r=2\cos (5\theta)=2\cos (5\theta)=r\\eq -r`

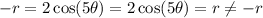
Therefore, the graph is not symmetric about the origin.