Question

The figure below shows a ray of light as it travels from media A to media B.The refractive index of media B to media A is

Answer 1

Given data:

* The angle of incidence in the medium A is,

`i=60^(\circ)`

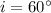
* The angle of refraction in medium B is,

`r=45^(\circ)`

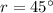
Solution:

According to the Snell's Law,

`\begin{gathered} n_A\sin (i)=n_B\sin (r) \\ (n_B)/(n_A)=(\sin (i))/(\sin (r)) \end{gathered}`

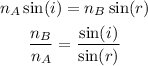
where n_B is the refractive index of medium B and n_A is the refractive index of medium B,

Substituting the known values,

`\begin{gathered} (n_B)/(n_A)=\frac{\sin (60^{\circ_{}})}{\sin (45^(\circ))} \\ (n_B)/(n_A)=(0.866)/(0.707) \\ (n_B)/(n_A)=1.225 \end{gathered}`

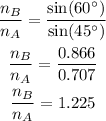
Thus, the ratio of refractive index of medium B to the refractive index of medium A is 1.225.