Question

A boat traveled 280 miles downstream and back. The trip downstream took 7 hours. The trip bck took 14 hours. Find the speed of the boat in still water and the speed of the current.

Answer 1

recall your d = rt, distance = rate * time

bearing in mind that the trip over, upstream, is the same distance as back, 280 miles.

if say, the boat has a speed rate of say "b", and the current has a speed rate of "c", so, when the boat was going upstream, it really wasn't going "b" fast, it was going "b-c" fast, because the stream is subtracting speed from it, because is going against the stream.

And when the boat was going downstream, is not going "b" fast either, is going "b+c" because, since it's going with the current, the current's rate is adding speed to it.


`\bf \begin{array}{lccclll} &\stackrel{miles}{distance}&\stackrel{mph}{rate}&\stackrel{hours}{time}\\ &------&------&------\\ Downstream&280&b+c&7\\ Upstream&280&b-c&14 \end{array} \\\\\\ \begin{cases} 280=7(b+c)\implies (280)/(7)=b+c\\ 40=b+c\implies 40-c=\boxed{b}\\ -------------\\ 280=14(b-c)\implies (280)/(14)=b-c\\ 20=b-c\\ ----------\\ 20=\left( \boxed{40-c} \right)-c \end{cases} \\\\\\ 20=40-2c\implies 2c=40-20\implies c=\cfrac{20}{2}`

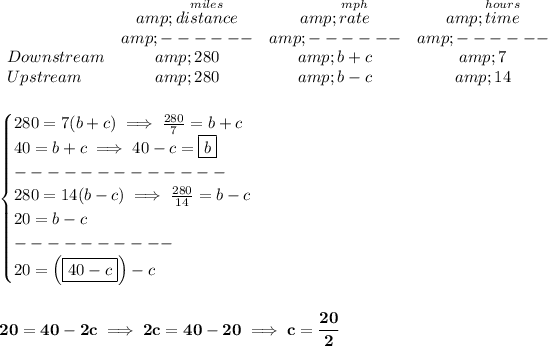
what's the speed of the boat? well, 40 - c = b.