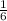Question

Find the common difference of the sequence shown. 1/6 , 1/3 , 1/2 , 2/3 , ... 1/12 1/6 1/3

Answer 1

I'll write my answer in here 1/6

Answer 2

The common difference of the sequence is
`(1)/(6)`

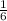
Explanation

The term "common difference" is telling us that our sequence is arithmetic. To find the common difference of an arithmetic sequence, we use the formula:
`d=a_(n)-a_(n-1)`

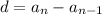
where

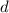`d` is the common difference

`a_(n)` is the current term in the sequence

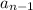`a_(n-1)` is the previous term in the sequence

In other words, the formula is telling us that to find the common difference, we subtract the previous term in the sequence form the current term in the sequence.

Let's find the difference for 1/6 , 1/3:

`a_(n)=(1)/(3)` and
`a_(n-1)=(1)/(6)`

`d=a_(n)-a_(n-1)`

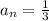`d=(1)/(3)-(1)/(6)`

`d=(1)/(6)`

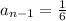
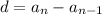
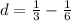
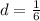
Let's make sure that the difference holds across the sequence by repeating the process for 1/3 , 1/2

`a_(n)=(1)/(2)` and
`a_(n-1)=(1)/(3)`

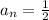`d=(1)/(2)-(1)/(3)`

`d=(1)/(6)`

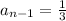
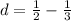
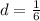
And finally, for 1/2 , 2/3

`a_(n)=(2)/(3)` and
`a_(n-1)=(1)/(2)`

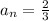`d=(2)/(3)-(1)/(2)`

`d=(1)/(6)`

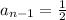
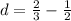
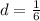
We can conclude that the common difference of the sequence shown is
`(1)/(6)`