Question

Find the volume of the cone if the heights of the solids are equal and the cross sectional areas at every level parallel to the respective bases are also equal. Round to the nearest hundredth.

A. 59.97
B. 93.46
C. 193.86
D. 280.37

Answer 1

B.93.46 cubic ft

Explanation:

We are given that

Height of solid=17 ft

Height of cone=Height of solids=17 ft

When the cross sectional areas at every level parallel to the respective bases are equal then the volume of both solids are equal.

Height of right triangle=8 ft

Hypotenuse of right triangle=9 ft

Base of right triangle=
`√(hypotenuse)^2-(height)^2)=√((9)^2-(8)^2)=√(17) ft`

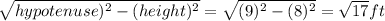
Area of base=Area of right triangle =
`(1)/(2)* base* height`

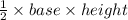
Area of base=
`(1)/(2)* √(17)* 8`

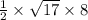
We know that Volume of pyramid=
`(1)/(3)(area\;of\;base)(height)`

Substitute the values in the given formula

Volume of cone=Volume of pyramid =
`(1)/(3)* (1)/(2)* √(17)* 8* 17=93.46 ft^3`

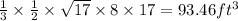
Hence, the volume of cone=93.46 cubic ft

Answer:B.93.46 cubic ft

Answer 2

Option B. 93.46 ft³

Explanation:

In the given question tow solids are given.

Their heights are same and the cross sectional areas at every level parallel to the respective bases are same which means total volume of solids are also same.

We have to find the volume of the cone.

We know the formula of volume of a pyramid
`V=(1)/(3)(Area of Base)(Height)`

Now area of the base = area of a right angle triangle =
`(1)/(2)(Base)(Height)`

Here height of the right angle triangle = 8 ft

and base of the triangle =
`\sqrt{Hypotenuse^(2)-height^(2)}=\sqrt{9^(2)-8^(2)}=√(81-64)=√(17)=4.12 ft`

Now area of base =
`(1)/(2)(4.12)(8)=16.49 ft^(2)`

Now volume of cone = volume of pyramid =
`(1)/(3)(16.49)(17)=(280.37)/(3)=93.46ft^(3)`

Therefore Option B. is the answer.