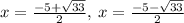Question

If the quadratic formula is used to solve 2x(x + 5) = 4, what are the solutions?

Answer 1

`x=(-5+√(33))/(2),\:x=(-5-√(33))/(2)`

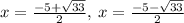
Explanation:

The given equation is
`2x(x+5)=4`

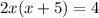
Distribute 2x over the parentheses

`2x^2+10x=4`

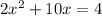
Subtract 4 to both sides of the equation

`2x^2+10x-4=0`

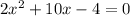
We can take 2 common and rewrite the equation as

`x^2+5x-2=0`

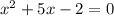
Apply the quadratic formula,
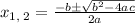`x_(1,\:2)=(-b\pm √(b^2-4ac))/(2a)`, we get

`x_(1,\:2)=(-5\pm √(5^2-4\cdot \:1\left(-2\right)))/(2\cdot \:1)`

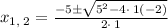
Simplifying we get

`(-5\pm√(33))/(2\cdot \:1)`

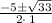
Thus, the solution to the given quadratic equation is

`x=(-5+√(33))/(2),\:x=(-5-√(33))/(2)`