Question

Solve the exponential equation. Round to three decimal place when necessary. 9^(x+4)=7^x

Answer 1

C. -34.972

Step-by-step explanation:

Given the equation:

`9^(x+4)=7^x​`

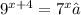
To solve for x, follow the steps below.

Step 1: Take the logarithm of both sides.

`\log (9^(x+4))=\log (7^x​)`

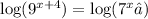
Step 2: Apply the index of a logarithm law stated below.

`\begin{gathered} \log (a^n)=n\log (a) \\ \implies\log (9^(x+4))=\log (7^x​) \\ (x+4)\log 9=x\log (7) \end{gathered}`

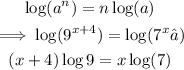
Step 3: Bring all the terms containing x together by dividing both sides by x log (9)

`\begin{gathered} ((x+4)\log(9))/(x\log(9))=(x\log(7))/(x\log(9)) \\ \implies(x+4)/(x)=(\log(7))/(\log(9)) \end{gathered}`

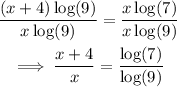
Step 4: Use a calculator to evaluate the right-hand side.

`(x+4)/(x)=0.885622`

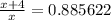
Step 5: Cross multiply and solve for x.

`\begin{gathered} x+4=0.885622x \\ x-0.885622x=-4 \\ 0.114378x=-4 \\ (0.114378x)/(0.114378)=(-4)/(0.114378) \\ x=-34.972 \end{gathered}`

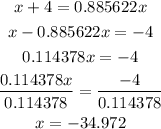
The value of x is -34.972 (Option C).