Question

What is the greatest possible integer value of x for which square root of x-5 is an imaginary number?

Answer 1

The answer is 4.

Starting with 4
= square root (4 - 5)
= square root (-1)
= imaginary

Hope this helps!

Answer 2

x = 4

Explanation:

Value of
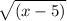`√((x-5))` will be imaginary. if
`√((x-5))` =
`√((-1))`

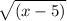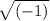
Since
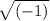`√((-1))` is not defined to square root will be imaginary.

In this question greatest possible integer value of x has been asked.

(x-5) will be negative if x<5 and the maximum value of x will be 4 above which (x-5) will be greater than zero.

Therefore, x = 4 is the maximum integer value of x for which square root of (x-5) is an imaginary number.