Let p be the total number of people.
Therefore,
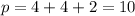
Let the number of people that waited for a particular time,x, be n.
Therefore, the probability, Pr(x), that a person waited for a time x is given by
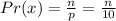
Now, we make a table as shown below
x | Number of people(n) | Pr(x) | xPr(x)
------------------------------------------------------------------------------------------
4 | 4 | 0.4 | 1.6
------------------------------------------------------------------------------------------
24 | 4 | 0.4 | 9.6
------------------------------------------------------------------------------------------
106 | 2 | 0.2 | 21.2
-------------------------------------------------------------------------------------------
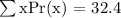
Therefore, the expected value is 32.4 minutes