Question

Can you help me with solving this problem please 8

Answer 1

yea but where is the problem ?????

Explanation:

Answer 2

- The question would like us to solve the following:

`8<p>- The solution is given below:</p>[tex]\begin{gathered} 88 \\ \\ \text{ Expand the bracket} \\ \\ 9x-x^2>8 \\ \\ \text{ Rewrite the inequality, we have:} \\ -x^2+9x-8>0 \end{gathered}`

- Now, we can factorize the expression as follows:

`\begin{gathered} -x^2+9x-8>0 \\ \text{ 9x can be rewritten as 8x + x} \\ -x^(2)+8x+x-8\gt0 \\ \\ \text{ Factorize,} \\ \\ x(-x+8)-1(-x+8)>0 \\ (-x+8)\text{ is common so we can factorize again,} \\ \\ (x-1)(8-x)>0 \end{gathered}`

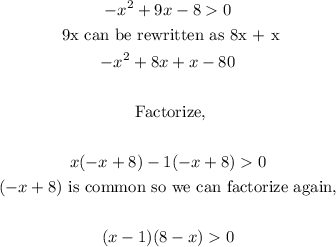
- Now, we need to decide where the solution region of the inequality is. The possible solution regions are

[tex]\begin{gathered} \text{ Region 1: }x\lt1 \\ \text{ Region 2: }1\lt x\lt8 \\ \text{ Region 3: }x>8 \\ \\ \text{ We simply need to choose the values that fall into any of these regions and test them in the } \\ \text{ original inequality for which ones are correct.} \\ \\ \text{ Region 1:} \\ \text{ Choosing }x=0,\text{ since, }x<1 \\ 88 \\ 8

- Thus, the solution to the inequality is:

[tex]1

Final Answer

The solution to the inequality is:

[tex]1