Question

A golf ball is dropped from a height of 30 ft to the pavement, and the rebound is one fourth the distance it drops. if after each descent it continues to rebound one fourth the distance dropped, what is the distance the ball has traveled when it reaches the pavement on its tenth descent?

Answer 1

The question deals with a sequence of movements of a golf ball falling and rebounding, which forms a geometric series. To find the total distance traveled by the ball on its 10th descent, we calculate the sum of the first 19 terms of this geometric progression.

Step-by-step explanation:

The student is asking about a geometric series problem, which involves a golf ball being dropped from a height and rebounding to a fraction of that height. The sequence of the distances covered by the ball forms a geometric progression.

Let's denote the initial height the ball is dropped from as a, which is 30 ft. The rebound height is one-fourth of the descent, so the rebound ratio, or common ratio r, is 1/4. The ball travels the initial height a plus the rebound distance each time it hits the pavement. This series continues with each rebound being one-fourth of the previous fall. We want to find the total distance traveled by the ball as it hits the pavement on its 10th descent.

The total distance traveled D after the ball hits the pavement for the 10th time is the sum of the first 10 terms of this geometric sequence. Using the formula for the sum of the first n terms of a geometric series,
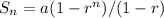`S_n = a(1-r^n)/(1-r)`, where n is the number of terms, we can calculate the total distance.

For 10 descents, we have n = 19 since each descent and rebound except

the last descent counts as two movements:

`S_(19) = 30(1-(1/4)^(19))/(1-(1/4))`

`S_(19) = 30(1-(1/4)^(19))/(3/4)`
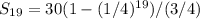
By calculating
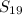`S_{19`, we find the total distance traveled when the ball hits the pavement on its 10th descent.

Answer 2

sum of a geometric sequcne
the ratio is 1/4 the initial height is 30

but we double it because it bounces down then up

but it doesn't bounce up on the first bounce so minus 30


sum of a geometric sequence where the first term is a1 and common ratio is r is

`S_n=(a_1(1-r^n))/(1-r)`
so

the distance it traveled after n bounces is

`S_n=2((30(1-((1)/(4))^n))/(1-(1)/(4)))-30`

so for n=10

`S_(10)=2((30(1-((1)/(4))^(10)))/(1-(1)/(4)))-30`

`S_(10)=2((30(1-((1)/(4^(10)))))/((3)/(4)))-30`
use your calculator

`S_(10)=49.9999999999`

so it traveled about 50ft