Question

G find an equation of the sphere with center (3, −10, 4) and radius 5. (x−3)2+(y+10)2+(z−4)2=25 use an equation to describe its intersection with each of the coordinate planes. (if the sphere does not intersect with the plane, enter dne.)

Answer 1

The Equation of the sphere with center (3, -10, 4) and radius 5 is correctly given as:


`(x-3)^2+(y+10)^2+(z-4)^2=5^2`,


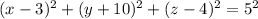
The x-y axis is the set of all points (ordered triples) of the form (x, y, 0), where x, y can be any point, but the z-coordinate is 0.

the intersection of the sphere and this plane is found by letting z=0:


`(x-3)^2+(y+10)^2+(z-4)^2=5^2\\\\(x-3)^2+(y+10)^2+(0-4)^2=5^2\\\\(x-3)^2+(y+10)^2+16=25\\\\(x-3)^2+(y+10)^2=9\\\\(x-3)^2+(y+10)^2=3^2`

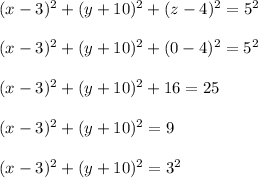
the last equation is the standard equation of the circle with center (3, -10) and radius 3.

Indeed, we expect the intersection of a sphere with a plane to be a circle.



Similarly the y-z plane is represented by (0, y, z) and the x-z plane by (x, 0, z),

The intersection of the sphere with the plane y-z is:


`(0-3)^2+(y+10)^2+(z-4)^2=5^2\\\\(y+10)^2+(z-4)^2=25-9=16=4^2`


and the intersection of the sphere with the x-z plane is :


`(x-3)^2+(0+10)^2+(z-4)^2=5^2\\\\(x-3)^2+(z-4)^2=25-100\ \textless \ 0`

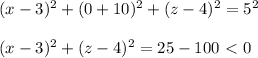
which makes no sense since the left hand side is positive (or at least 0).. This means that there is no intersection of the sphere with the x-z plane.


Answer:

intersection with the x-y plane:
`(x-3)^2+(y+10)^2=3^2`

intersection with the y-z plane:
`(y+10)^2+(z-4)^2=4^2`

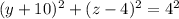
intersection with the x-y plane: none