Question

In exercises 83–86, verify that the intermediate value theorem applies to the indicated interval and find the value of guaranteed by the theorem.

Answer 1

The intermediate value theorem states that suppose f is a function continuous on every point of the interval [a, b], for any L between the values f(a) and f(b), there exist at least one number, c, in [a, b] for which f(c) = L.

83.
Given

`f(x)=x^2+x-1`
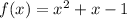
on the interval [0, 5], with f(c) = 11


`f(0)=0^2+0-1=-1`
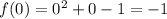
and

`f(5)=5^2+5-1=25+4=29`
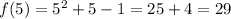
Clearly, f(c) = 11 is between f(0) = -1 and f(5) = 29

Thus, the intermediate value theorem is satisfied.

To find the value of c, we solve the equation

`c^2+c-1=11`
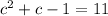
as follows:

`c^2+c-1=11 \\ \\ c^2+c-12=0 \\ \\ (c-3)(c+4)=0 \\ \\ c=3 \ or \ -4`

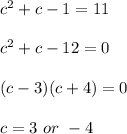
Because, c is in the interval [0, 5], therefore, the value of c is 3.


84.
Given

`f(x)=x^2-6x+8`
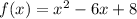
on the interval [0, 3], with f(c) = 0


`f(0)=0^2-6(0)+8=8`
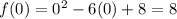
and

`f(3)=3^2-6(3)+8=9-18+8=-1`
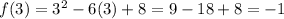
Clearly, f(c) = 0 is between f(0) = 8 and f(3) = -1

Thus, the intermediate value theorem is satisfied.

To find the value of c, we solve the equation

`c^2-6c+8=0`
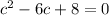
as follows:

`c^2-6c+8=0 \\ \\ (c-4)(c-2)=0 \\ \\ c=4 \ or \ 2`

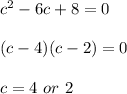
Because, c is in the interval [0, 3], therefore, the value of c is 2.


85.
Given

`f(x)=x^3-x^2+x-2`
on the interval [0, 3], with f(c) = 4


`f(0)=0^3-0^2+0-2=-2`
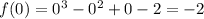
and

`f(3)=3^3-3^2+3-2=27-9+1=19`
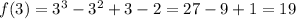
Clearly, f(c) = 4 is between f(0) = -2 and f(3) = 19

Thus, the intermediate value theorem is satisfied.

To find the value of c, we solve the equation

`c^3-c^2+c-2=4`
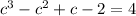
as follows:

`c^3-c^2+c-6=0 \\ \\ (c^2+c+3)(c-2)=0 \\ \\ c=2`

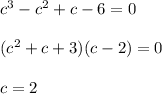
Therefore, the value of c is 2.


86.
Given

`f(x)= (x^2+x)/(x-1)`
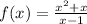
on the interval
`\left[ (5)/(2), \ 4\right]`, with f(c) = 6


`f\left((5)/(2)\right)= (\left((5)/(2)\right)^2+\left((5)/(2)\right))/(\left((5)/(2)\right)-1)= ( (25)/(4)+ (5)/(2) )/( (3)/(2) ) = (35)/(4) \cdot (2)/(3) =5 (5)/(6)`
and

`f(4)= (4^2+4)/(4-1)= ( 16+ 4 )/( 3 ) = (20)/(3)=6 (2)/(3)`
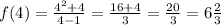
Clearly, f(c) = 6 is between
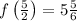
`f\left((5)/(2)\right)= 5 (5)/(6)` and
`f(4)=6 (2)/(3)`

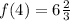
Thus, the intermediate value theorem is satisfied.

To find the value of c, we solve the equation

`(c^2+c)/(c-1)=6`
as follows:

`c^2+c=6(c-1)=6c-6 \\ \\ \Rightarrow c^2-5c+6=0 \\ \\ \Rightarrow(c-2)(c-3)=0 \\ \\ \Rightarrow c=2 \ or \ 3`

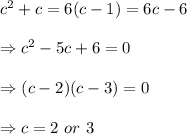
Because, c is in the interval
`\left[ (5)/(2), \ 4\right]`, therefore, the value of c is 3.