The value of the original investment at the end of year 4 is $12,625.
To find the value of the original investment at the end of year 4, we will use the compound interest formula, which is given by:
![\[ A = P \left(1 + (r)/(n)\right)^(nt) \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/high-school/3oai866h0yu84hxh2lb1.png)
where:
- A is the amount of money accumulated after n years, including interest.
- P is the principal amount (the initial amount of money).
- r is the annual interest rate (in decimal form).
- n is the number of times that interest is compounded per year.
- t is the time the money is invested for, in years.
In this case, we have the following information:
- Principal amount, P, is $10,000.
- Annual interest rate, r , is 6% or 0.06 in decimal form.
- Interest is compounded annually, so n is 1.
- We want to find the amount at the end of year 4, so t is 4.
Now, we just need to plug these values into the compound interest formula:
![\[ A = 10000 \left(1 + (0.06)/(1)\right)^(1 \cdot 4) \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/jhofqr4w12qq6rafy6jc.png)
![\[ A = 10000 \left(1 + 0.06\right)^4 \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/2mod286y3v7s2xp401ny.png)
![\[ A = 10000 \left(1.06\right)^4 \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/ikso6lfmcws8qetayhxf.png)
Now, let's calculate
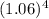 :
:
![\[ (1.06)^4 = 1.06 * 1.06 * 1.06 * 1.06 \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/y7vucrmoo7p569phqdhk.png)
![\[ (1.06)^4 \approx 1.2625 \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/sj4jyxb2g5liwemuhuto.png) (rounded to four decimal places)
(rounded to four decimal places)
Multiplying this by the principal:
![\[ A = 10000 * 1.2625 \]](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/lzrqgzwrgoexgo1tbkta.png)
A = 12625