Hi!
Okay, so let's start with swapping all of the variables.
x = -6y + 12.
We'll start with subtracting both sides by 12. Our goal is to isolate y, and we do so by doing the inverse of the operation on each value.
Since 12 is positive, the inverse of being positive is negative. So, we shall subtract!
x - 12 = -6y + 12 - 12.
Which leaves us with x - 12 = -6y.
Since the -6 is multiplying our variable, the inverse of multiplication is division, so we shall divide both sides by -6.
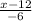
= -6y / -6.
Which leaves us with
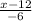
= y.
Our final answer is:
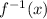
=
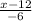
.
Hopefully, this helps! =)