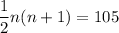Question

Half of the product of two consecutive numbers is 105. Which equation can be used to solve for n, the smaller of the two numbers?

Answer 1

Let the smaller number be n:
Therefore 1/2 * n(n+1) = 105
n^2 + n = 210
n^2 + n - 210 =0
Use your preferred method to solve the quadratic, I'll factorise this since this is easy to factorise.
Two numbers':
product gives -210
summation gives 1
Therefore (n+15)(n-14)=0
So the smaller number n is either -15 or 14.

Answer 2

Answer with Step-by-step explanation:

We are given that:

Half of the product of two consecutive numbers is 105.

Let smaller number be n

Then, larger number will be n+1

`(1)/(2)n(n+1)=105`

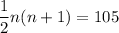
Multiplying by 2 on both sides, we get

n(n+1)=210

n²+n=210

n²+n-210=0

On splitting the middle term

n²+15n-14n-210=0

n(n+15)-14(n+15)=0

(n-14)(n+15)=0

either n-14=0 or n+15=0

either n=14 or n= -15

When n=14, n+1=15

when n= -15, n+1= -14

Hence, equation used to solve for n was:

`(1)/(2)n(n+1)=105`