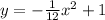Question

please help me do this i think i’mdoing it right but i’m not sure The graph shows a parabola and its focus. Write the equation of the parabola in vertex form.

Answer 1

Step 1

Write the parabola in vertex form eqaution

`(x-h)^2=-4a(y-k)`

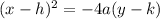
where

`\begin{gathered} h=0=x-\text{coordinate of the vertex} \\ k=1=y-\text{coordinate of the vertex} \end{gathered}`

Step 2

Find the required equation

The distance between the vertex and the focus = a

Therefore,

`\begin{gathered} \text{The vertex=(0,1)} \\ \text{The focus= (0,-2)} \end{gathered}`

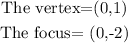
Hence with the formula for the distance between two points we have

`\begin{gathered} D=\sqrt[]{(0-0)^2+(-2-1)^2}^{}_{} \\ D=\sqrt[]{0^2+(-3)^2} \\ D=\sqrt[]{0+9} \\ D=\sqrt[]{9} \\ D=3 \\ a=D=3 \end{gathered}`

Step 3

Get the required equation by substitution

`\begin{gathered} (x-h)^2=-4(a)(y-k) \\ (x-0)^2=-4(3)(y-1) \\ x^2=-12(y-1) \end{gathered}`

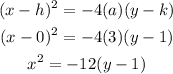
Hence in vertex form, the equation of the parabola will be

`y=-(1)/(12)x^2+1`

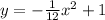
The answer is written as;

`y=-(1)/(12)x^2+1`