Not necessarily.
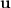
and

may be linearly dependent, so that their span forms a subspace of
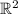
that does not contain every vector in
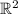
.
For example, we could have

and

. Any vector
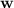
of the form
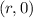
, where
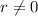
, is impossible to obtain as a linear combination of these
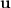
and

, since
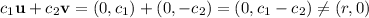
unless
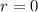
and
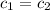
.