Question

Why do you think the area swept out by a planet in a given period of time remains constant, even as the planet speeds up and slows down?

Answer 1

Not sure this is entirely right but hey why not, right. A planet orbiting a star orbits in an ellipse. Sometimes it's closer to the star and sometimes it's further. When it's closer to the star, the gravity on the planet from the star is stronger, so the planet speeds up. The area the planet sweeps over is equal because when it speeds up the length covered along the orbital path is greater, but it is also closer to the star, and that dimension is decreased. And because of our very intelligently designed and organized universe, these two factors cancel each other out perfectly
Hope I helped in some way!

Answer 2

Since there is no torque on the planet with respect to position of Sun

So the angular momentum of the planet is always constant

hence the rate of change in area with respect to sun is always constant

Step-by-step explanation:

As we know that rate of area swept by the planet is given as

`v_a = (dA)/(dt)`

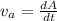
here we know that small area swept by the planet is given as

`dA = (1)/(2)r^2\theta`

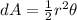
now rate of area swept by the planet is given as

`(dA)/(dt) = (1)/(2)r^2(d\theta)/(dt)`

`(dA)/(dt) = (1)/(2)r^2\omega`

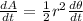
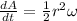
so we have

`(dA)/(dt) = (1)/(2m)(mr^2\omega)`

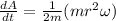
here we know that angular momentum of the planet with respect to sun is given as

`L = mr^2\omega`

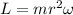
so we have

`(dA)/(dt) = (L)/(2m)`

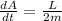
since we know that there is no torque on the system of planet with respect to sun

So angular momentum of the planet will remain constant

hence we can say

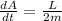`(dA)/(dt) = (L)/(2m)` = constant always