Question

If f(x) = x^4 − x^3 + x^2 and g(x) = −x^2, where x ≠ 0, what is (f ⁄g)(x)?

Answer 1

The correct answer is

`((f)/(g))(x)=-x^2+x-1`

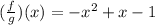
To solve this, first let's write the division:

`f(x)=x^4-x^3+x^2,g(x)=-x^2\Rightarrow((f)/(g))(x)=(x^4-x^3+x^2)/(-x^2)`

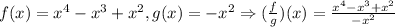
Now we can factor out a x^2 on the top and the bottom of the expression:

`((f)/(g))(x)=(x^4-x^3+x^2)/(-x^2)\Rightarrow((f)/(g))(x)=(x^2(x^2-x+1))/(x^2(-1))`

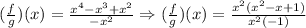
Now we can cancel out and divide by (-1), or the same thing, multiply by (-1):

`((f)/(g))(x)=(x^2(x^2-x+1))/(x^2(-1))=-(x^2-x+1)=-x^2+x-1`

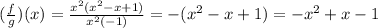
Then the answer is (f/g)(x) = -x^2 + x - 1. That's the third option