Question

Find the value of y, given that m<KLM = 135

Answer 1

I think this is right

Answer 2

the value of y is, 5.5

Step-by-step explanation:

GIven:
`m\angle KLM=135^(\circ)`

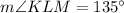
Linear pairs is a pair of adjacent angles formed when two lines intersect.

In the figure,
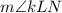`m\angle kLN` and
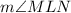`m\angle MLN` forms a linear pair.

then,
`m\angle KLM = m\angle KLN+m\angle MLN`.

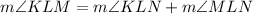Substitute the values of
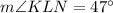`m\angle KLN= 47^(\circ)` and
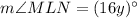`m\angle MLN= (16y)^(\circ)` in above equation, to find the value of y;

⇒
`135^(\circ)=47^(\circ)+(16y)^(\circ)` or

`16y^(\circ) =135^(\circ)-47^(\circ)`

Simplify:

`16y^(\circ) =88`

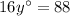
Divide 16 on both sides of an equation:

`(16y)/(16) =(88)/(16)`

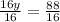
Simplify:

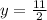`y=(11)/(2)` or y=5.5

Therefore, the value of y =
`(11)/(2)` or y=5.5.