Question

Two sumo wrestlers run into each other. One wrestler has a mass of 120kg and the other (sumo wrestler 2) has a mass of 130kg. Sumo wrestler 1 runs 4.20 m/s in the positive direction at sumo wrestler 2 who is running 4 m/s in the negative direction. After the collision, sumo wrestler 1 has a velocity of -6 m/s. What was Sumo wrestler 2’s final velocity?

Answer 1

Sumo wrestler 2’s final velocity was + 5.42 m/s.

Step-by-step explanation:

Here is the information we know about the wrestlers.

Before the collision:

Sumo Wrestler 1: 120 kg, velocity = + 4.20 m/s

Sumo Wrestler 2: 130 kg, velocity = - 4.00 m/s

After the collision:

Sumo Wrestler 1: 120 kg, velocity = -6.00 m/s

Sumo Wrestler 2: 130 kg, velocity = unknown

Now, the law of conservation of momentum demands that

`m_1v_1+m_2v_2=m_1v_(f1)+m_2v_(f2)`

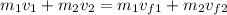
where

m1 = mass of wrestler 1

m2 mass of wrestler 2

v1 = inital velocity of wrestler 1

v2 = initial velocity of wrestler 2

vf1 = final velocity of wrestler 1

vf2 = final velocity of wrestler 2

Now in our case

m1 = 120 kg

m2 = 130 kg

v1 = + 4.20 m/s

v2 = - 4.0 m/s

vf1 = -6.0 m/s

vf2 = unknown

Therefore, putting these values into the above equation gives

`120\cdot4.20+130\cdot(-4.0)=120\cdot(-6.0)+130v_(f2)`

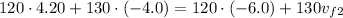
which simplifies to give us

`-16=-720+130v_(f2)`

adding 720 to both sides gives

`-16+720=130v_(f2)`
`\Rightarrow704=130v_(f2)`
`v_(f2)=(704)/(130)`
`\boxed{v_{\mleft\{f2\mright\}}=5.42m/s\text{.}}`

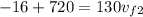
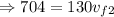
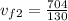
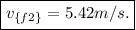
Hence, the final velocity of Sumo wrestler 2 is 5.42 m/s.