Question

Four points are always coplanar if

Answer 1

For example, three points are always coplanar, and if the points are distinct and non-collinear, the plane they determine is unique. However, a set of four or more distinct points will, in general, not lie in a single plane. Two lines in three-dimensional space are coplanar if there is a plane that includes them both.

Answer 2

Four points are always coplanar if triple scalar product is zero.

Explanation:

We have four points and we find the condition for four points are coplanar.

Let A,B,C and D are four points .We have to find Vector AB, AC and AD.

Then we find triple scalar product of vectors AB,AC and AD.

Triple scalar product=
`vec{AB}.(\vec{AC*AD})`

To find triple scalar product we use determinant

Suppose A(1,0,-1),B(0,2,3),C(-2,1,1) and D(4,2,3) are four points .

We shall prove that A,B,C and D are coplanar.

We find vector AB,AC and AD

`\vec{AB}`=Coordinate of B -coordinate of A=
`-1\hat{i}+2\hat{j}+4\hat{k}`

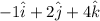
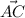`\vec{AC}`=Coordinate of C-coordinate of A=
`-3\hat{i}+\hat{j}+2\hat{k}`

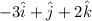
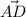`\vec{AD}`=Coordinate of D- coordinate of A=
`3\hat{i}+2\hat{j}+4\hat{k}`

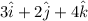
Now , we find triple scalar product

`\vec{AB}.(\vec{AC}*\vec{AD})=\begin{vmatrix}-1&2&4\\-3&1&2\\3&2&4\end{vmatrix}`

Expand alon
`R_1`

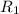
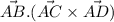`\vec{AB}.(\vec{AC}*\vec{AD})`=-1(4-4)-2(-12-6)+4(-6-3)

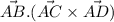`\vec{AB}.(\vec{AC}*\vec{AD})`=0+36-36=0

Hence, triple scalar product is zero therefore, four points A,B,C and D are coplanar.

Four points are always coplanar if triple scalar product is zero.