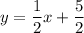Question

The point-slope form of the equation of the line that passes through (–9, –2) and (1, 3) is y – 3 = (x – 1). What is the slope-intercept form of the equation for this line?

y =1/2 x + 2
y = 1/2x – 4
y = 1/2x + 5/2
y = 1/2x – 7/2

Answer 1

(-9,-2) (1,3)
slope = (3 - (-2) / (1 - (-9) = 5/10 = 1/2

y - y1 = m(x - x1)
slope(m) = 1/2
(1,3)...x1 = 1 and y1 = 3
sub
y - 3 = 1/2(x - 1)
y - 3 = 1/2x - 1/2
y = 1/2x - 1/2 + 3
y = 1/2x - 1/2 + 6/2
y = 1/2x + 5/2 <=== slope intercept form

Answer 2

Answer:
`y=(1)/(2)x+(5)/(2)`

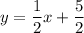
Explanation:

Equation of a line passing through points (a,b) and (c,d) is given by :-

`(y-b)=(d-b)/(c-a)(x-a)`

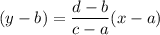
Similarly, the equation of line passing through (-9, -2) and (1, 3) is given by :-

`(y-3)=(3-(-2))/(1-(-9))(x-1)`

`(y-3)=(3+2)/(1+9))(x-1)`

`(y-3)=(5)/(10)(x-1)`

`(y-3)=(1)/(2)(x-1)`

`(y-3)=(1)/(2)x-(1)/(2)`

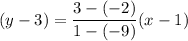
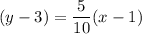
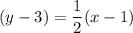
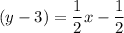
Add 3 both sides , we get

`y=(1)/(2)x-(1)/(2)+3`

`y=(1)/(2)x+((2)(3)-1)/(2)`

`y=(1)/(2)x+(5)/(2)`

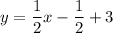
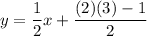
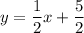
Hence, he slope-intercept form of the equation for this line :

`y=(1)/(2)x+(5)/(2)`