Question

find the area of the shaded region. The radius of each circle is r. If twocircles are shown, r is the radius of the smaller circle and R is the radius of the largercircle.

Answer 1

We have to calculate the area of the shaded region.

We can do it in two steps.

We can calculate the difference between the outer circle and the inner circle.

Then, we calculate the proportional area according to the fraction of the circunference covered by the arc.

We can express the difference between the two complete circles as:

`\begin{gathered} A=A_o-A_i \\ A=\pi R^2-\pi r^2_{} \\ A=\pi(R^2-r^2) \\ A=\pi(12^2-9^2) \\ A=\pi(144-81) \\ A=\pi\cdot63 \\ A\approx197.92cm^2 \end{gathered}`

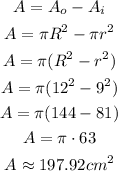
As the circle is not complete, we have to calculate the area of the arc as the fraction of the complete circle. This fraction will be equal to the angle of the arc (360-60 = 300°) divided by the total circumference (360°).

We can then calculate the area of the shaded area as:

`\begin{gathered} A_(sh)=f\cdot A \\ A_(sh)=(300)/(360)\cdot197.92 \\ A_(sh)=(5)/(6)\cdot197.92 \\ A_(sh)=164.93 \end{gathered}`

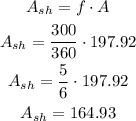
Answer: the shaded area is equal to 164.93 cm².