Question

The parent function f(x) = log5x has been transformed by reflecting it over the x-axis, stretching it vertically by a factor of two and shifting it down three units. Which function is representative of this transformation? g(x) = log5(2x) - 3 g(x) = log5(-2x) + 3 g(x) = -2log5(x) - 3 g(x) = 2log5(x) + 3

Answer 1

To reflect it over the x axis, all y units get multiplied by -1, so we multiply the equation by -1. After that, to stretch it vertically, we multiply it by that factor, which is 2. Right now , we have -2log(5x). Lastly, we shift it down 3 units by subtracting 3 from the overall equation, resulting in  -2log(5x)-3

Answer 2

Option 3 -
`g(x)=-2log_5 (x)-3`

Explanation:

Given : The parent function
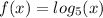`f(x)=log_5 (x)` has been transformed by reflecting it over the x-axis, stretching it vertically by a factor of two and shifting it down three units.

To find : Which function is representative of this transformation.

Solution : The parent function
`y=log_5 (x)`

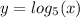
• Transformed by reflecting it over the x-axis.

Transformation over x-axis is f(x,y)→f(x,-y)

`-y=log_5 (x)`

`y=-log_5 (x)`

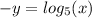
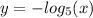
• Stretching it vertically by a factor of two

Stretching it vertically means multiply the factor by output constant given.

Multiply the parent function by 2.

`y=-2log_5 (x)`

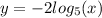
• Shifting it down three units.

Shifting downwards means f(x)→f(x)-b , function shift downward by b unit.

`y=-2log_5 (x)-3`

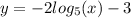
Therefore, The new function formed is
`g(x)=-2log_5 (x)-3`

So, Option 3 is correct.