Question

Select the graph and the description of the end behavior of f(x) = −x3 − 2.

Answer 1

the answer is the fourth one

Answer 2

Answer: Option 4 is correct

Step-by-step explanation:

End behaviour of graph can be check by following rules

Case 1: even degree and positive leading coefficient

`x\rightarrow -\infty`
`f(x)\rightarrow \infty`

`x\rightarrow \infty`
`f(x)\rightarrow \infty`

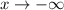
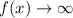
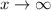
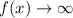
Case2: Even degree and negative leading coefficient

`x\rightarrow -\infty`
`f(x)\rightarrow -\infty`

`x\rightarrow \infty`
`f(x)\rightarrow -\infty`

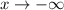
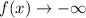
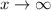
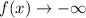
Case 3: odd degree and positive leading coefficient

`x\rightarrow -\infty`
`f(x)\rightarrow -\infty`

`x\rightarrow \infty`
`f(x)\rightarrow \infty`

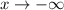
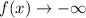
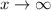
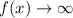
Case4: Odd degree and negative leading coefficient

`x\rightarrow -\infty`
`f(x)\rightarrow \infty`

`x\rightarrow \infty`
`f(x)\rightarrow -\infty`

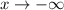
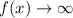
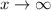
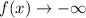
Here we have a case of odd degree and negative leading coefficient here when
`x\rightarrow -\infty`
`f(x)\rightarrow \infty`

`x\rightarrow \infty`
`f(x)\rightarrow -\infty`

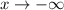
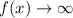
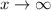
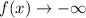
Hence, Option 4 is correct