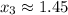Question

Use Newton's method to approximate a root of the equation 4x ^ 7 + 2x ^ 4 + 2 = 0 as follows. Let x_{1} = 2 be the initial approximation The second approximation is x_{2}

Answer 1

Given the equation:

`4x^7+2x^4+2=0`

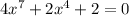
You need to remember that Newton's method to approximate a root of the equation provides this formula:

`x_(n+1)=x_n-(f(x_n))/(f^(\prime)(x_n))`

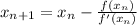
In this case:

`f(x_n)=4x^7+2x^4+2`

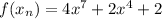
Then, you need to derivate it, in order to find:

`f^(\prime)(x_n)`

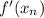
Use these Derivative Rules:

`\begin{gathered} (d)/(dx)(x^n)=nx^(n-1) \\ \\ (d)/(dx)(k)=0 \end{gathered}`

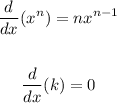
Where "k" is a constant.

You get:

`f^(\prime)(x_n)=(4)(7)x^6+(2)(4)x^3+0`
`f^(\prime)(x_n)=28x^6+8x^3`

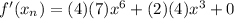
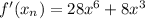
• Knowing that:

`x_1=2`

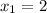
You can set up that:

`x_2=2-(4x^7+2x^4+2)/(28x^6+8x^3)`

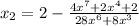
Substitute the given value of "x" and evaluate, in order to find the second approximation:

`\begin{gathered} x_2=2-(4(2)^7+2(2)^4+2)/(28(2)^6+8(2)^3) \\ \\ x_2=(1583)/(928) \end{gathered}`

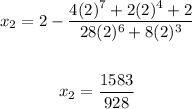
• Now you can set up that:

`x_3=(1583)/(928)-(4x^7+2x^4+2)/(28x^6+8x^3)`

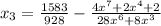
Then, substituting the corresponding x-value and evaluating, you get:

`x_3=(1583)/(928)-(4((1583)/(928))^7+2((1583)/(928))^4+2)/(28((1583)/(928))^6+8((1583)/(928))^3)`
`x_3\approx1.45`

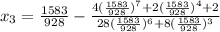
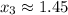
Hence, the answers are:

• Second approximation:

`x_2=(1583)/(928)`

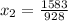
• Third approximation:

`x_3\approx1.45`