Question

What is the area of the shaded portion of the circle?

1. (16pie-32) in^2
2.(16pie-8) in^2
3.(64pie-32)in^2
4.(64pie-8)in^2

Answer 1

The angle between the lines in 90 degrees so the area of the whole sector is 1/4 of a circle

= 1/4 * pi * 8^2

The area of the triangle = 1/2 * 8 * 8 = 32

so area of the shaded segment = (16pi - 32) in^2

choice 1.

Answer 2

the answer is the first option

`(16\pi\ -32)\ in^(2)`

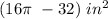
Explanation:

we know that

The area of the shaded portion of the circle is equal to the area of a quarter circle minus the area of the right triangle

Step 1

Find the area of a quarter circle

`A=(1)/(4)\pi r^(2)`

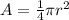
we have

`r=8\ in`

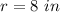
substitute

`A=(1)/(4)\pi (8)^(2)=16\pi\ in^(2)`

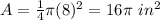
Step 2

Find the area of the right triangle

we know that

the area of the triangle is equal to

`A=(1)/(2)bh`

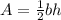
in this problem we have

`b=h=8\ in`

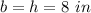
substitute

`A=(1)/(2)(8)^(2)=32\ in^(2)`

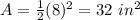
Step 3

Find the area of the shaded portion

Remember that

The area of the shaded portion of the circle is equal to the area of a quarter circle minus the area of the right triangle

`A=(16\pi\ -32)\ in^(2)`