Given that
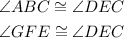
C is the point of intersection between AG and BD while E is the point of intersection between AG and DF
To prove the triangle ABC is similar to the triangle GEF
From the given figure, it is seen that
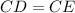
Therefore,
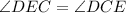
Since
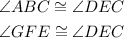
Then,
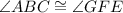
In the triangle ABC and the triangle GFE, two angles are congruent.
Therefore,
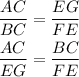
Similarly,
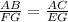
Thus,
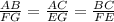
Hence, the triangle ABC is similar to the triangle GEF