Sounds like you're asked to find

such that
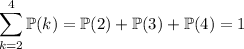
In other words, find

that satisfies
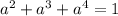
We can factorize this as
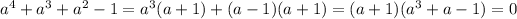
In order that
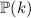
describes a probability distribution, require that

for all
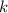
, which means we can ignore the possibility of

.
Let

.
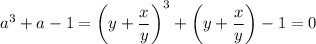
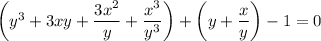
Multiply both sides by
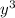
.
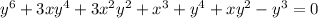
We want to find
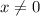
that removes the quartic and quadratic terms from the equation, i.e.
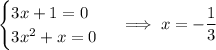
so the cubic above transforms to
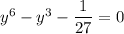
Substitute
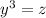
and we get
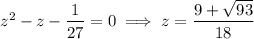
![\implies y=\sqrt[3]{(9+√(93))/(18)}](https://img.qammunity.org/2018/formulas/mathematics/college/i0su26gobzfmx381ooi32qlqjqysj3rt42.png)
![\implies a=\sqrt[3]{(9+√(93))/(18)}-\frac13\sqrt[3]{(18)/(9+√(93))}](https://img.qammunity.org/2018/formulas/mathematics/college/2eo9da63eg7n7n27j6gusbnobfjmw4vaiw.png)