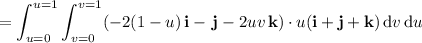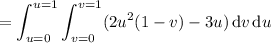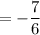Question

Use stokes' theorem to compute z c ~f d~s where ~f(x; y; z) = y2~i + z2~j + x~k and the curve c is the triangle in 3-space with vertices at (1; 0; 0), (0; 1; 0), and (0; 0; 1). hints: (a) for the surface s needed in stokes' theorem, use the part of the plane x + y + z = 1 that lies in the rst octant. (b) that plane can be written parametrically as (x; y) = hx; y; 1 ???? x ???? yi. (c) make sure you have the upward pointing normal!

Answer 1

By Stoke's theorem, the line integral of
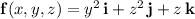
`\mathbf f(x,y,z)=y^2\,\mathbf i+z^2\,\mathbf j+z\,\mathbf k` along
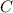
`C` (presumably the *boundary* of the triangle, and not the triangle itself)


`\displaystyle\int_C\mathbf f\cdot\mathrm d\mathbf r`

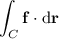
is given by the surface integral of
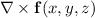
`\\abla*\mathbf f(x,y,z)` along the surface with boundary
`C`,


`\displaystyle\iint_S(\\abla*\mathbf f)\cdot\mathrm d\mathbf S`

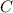
First, compute the curl of
`\mathbf f`:


`\\abla*\mathbf f=-2z\,\mathbf i-\,\mathbf j-2y\,\mathbf k`

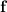
Not sure what kind of parameterization you're given for
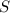
`S`, but you can use


`\mathbf s(u,v)=(1-u)\,\mathbf k+u(1-v\,\mathbf i+v\,\mathbf j)=(u-uv)\,\mathbf i+uv\,\mathbf j+(1-u)\,\mathbf k`

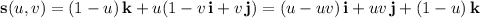
where
`(u,v)\in[0,1]*[0,1]`. Then


`\mathbf s_u*\mathbf s_v=u(\mathbf i+\mathbf j+\mathbf k)`

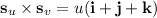
So the surface integral is equivalent to


`\displaystyle\iint_S(\\abla*\mathbf f)\cdot\mathrm d\mathbf S=\int_(u=0)^(u=1)\int_(v=0)^(v=1)(-2z(u,v)\,\mathbf i-\,\mathbf j-2y(u,v)\,\mathbf k)\cdot u(\mathbf i+\mathbf j+\mathbf k)\,\mathrm dv\,\mathrm du`

`\displaystyle=\int_(u=0)^(u=1)\int_(v=0)^(v=1)(-2(1-u)\,\mathbf i-\,\mathbf j-2uv\,\mathbf k)\cdot u(\mathbf i+\mathbf j+\mathbf k)\,\mathrm dv\,\mathrm du`

`\displaystyle=\int_(u=0)^(u=1)\int_(v=0)^(v=1)(2u^2(1-v)-3u)\,\mathrm dv\,\mathrm du`

`=-\frac76`